Modelo Hidrogeológico

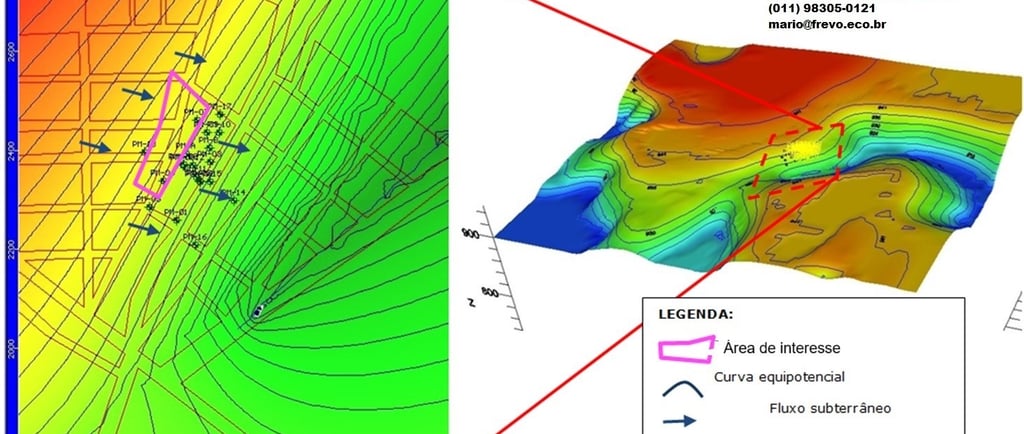
A caracterização dos aquíferos, a quantificação dos fenômenos de fluxo e de transporte, é fator fundamental no planejamento e gerenciamento dos recursos hídricos subterrâneos. Esta quantificação pode ser executada de diversas maneiras, desde medidas de campo a modelagem matemática.

Medidas de campo normalmente são pontuais (nível d’água em um poço, permeabilidades em um ponto ou litotipo, etc.), e como as águas subterrâneas movem-se, em média, alguns centímetros por ano, muitas vezes são necessários alguns anos de estudo para a caracterização do comportamento do aquífero.

Assim, apesar das medições diretas de campo serem a mais acuradas, raramente podem ser utilizadas sozinhas, devido seus altos custos e longos prazos de execução, além da impossibilidade de serem aplicadas em prognósticos (impacto de lixão, mineração, etc.).

Atualmente, o mais frequente é a representação artificial dos sistemas aquíferos através da utilização de modelos matemáticos utilizando equações de conservação de massa para simulação de fluxo e transporte de contaminantes, baseados nas propriedades físico-químicas medidas e inferidas do local. O desenvolvimento dos computadores pessoais com elevada capacidade de memória e velocidade de cálculo fez com que esta ferramenta seja amplamente utilizada, não sendo necessário o conhecimento de programação e domínio dos cálculos matemáticos envolvidos na modelagem. Não obstante, é vital a compreensão do modelo conceitual do cenário hidrogeológico a ser modelado.

A aplicação de modelos matemáticos objetiva representar o cenário hidrogeológico em questão, geralmente de maneira simplista, visando fornecer subsídios quantitativos em conjunto com os dados de campo e a experiência do profissional que o aplica para a tomada de decisões técnicas.

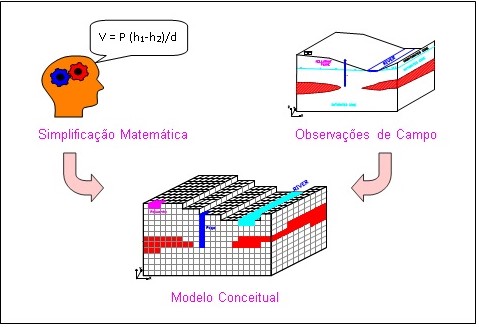
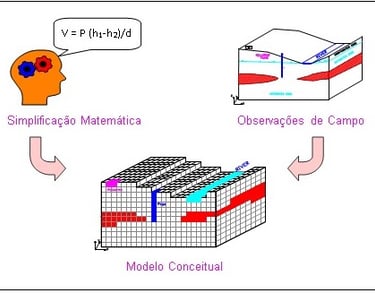
No entanto, cabe destacar que os modelos matemáticos não são a solução para todos os problemas hidrogeológicos, e sim, apenas mais uma poderosa ferramenta para o uso dos hidrogeólogos. Os modelos apresentam resultados consequentes de uma visão simplificada da hidrogeologia em função dos dados coletados, conforme ilustra a Figura 1. Mas estes resultados serão ponderados em função de todos os dados considerados.

Figura 1 - Modelos matemáticos, uma visão simplificada da realidade

Assim, os modelos possibilitam a análise de uma gama muito grande de informações em um tempo curto, possibilitando a tomada de decisões com melhor embasamento técnico e científico, apesar de, ainda, imperfeito.

Os modelos matemáticos podem ser aplicados a, entre outros objetivos, para(CLEARY, 1989 e 1991, ANDERSON & WOESSNER 1994, WHB 1998):

1 - Entendimento do comportamento hidrogeológico regional.

2 - Gerenciamento dos recursos hídricos subterrâneos:

a) locação de poços tubulares;

b) determinação do melhor regime de bombeamento;

c) delimitação de zonas de proteção e interferência entre poços;

3 - Prognósticos:

a) rebaixamento;

b)transporte de contaminante e respectiva concentração no tempo e espaço.

4 - avaliação de projetos de remediação:

a) avaliação de risco;

b) comparação e otimização de sistemas de remediação;

c) determinação do projeto técnico básico de remediação.

Basicamente os modelos numéricos de fluxo irão calcular, de uma maneira geral, a carga hidráulica a cada intervalo de tempo em todos os nós, isto é, a variável dependente. A partir da carga hidráulica, são calculadas as velocidades de percolação, através da lei de Darcy. A apresentação normalmente é feita na forma gráfica de contorno, produzindo o mapa potenciométrico.

Diversos outros resultados podem ser conseguidos através do cruzamento dos dados, como por exemplo, na delineação de áreas de proteção de poços, onde o contorno é estabelecido em função do tempo de trânsito usando a distribuição de cargas, da condutividade hidráulica, porosidade efetiva e a lei de Darcy. No caso de estudos de transporte de partículas, as velocidades são calculadas em cada nó através da diferenciação numérica das cargas.

Assim, para a formulação do modelo conceitual deve-se definir a área de interesse e as condições iniciais e de contorno do modelo.

Para a resolução da equação numérica faz-se necessário a definição de uma condição inicial para o tempo igual a zero (h = hx,y,z,0). Segundo CLEARY (1989) esta informação normalmente é desconhecida, e muitos modeladores utilizam uma carga constante média. A fim de minimizar interferências de possíveis definições de carga constante errônea, é recomendável que a definição desta no modelo seja o mais distante possível da área de interesse (MARCELINO, 1997).

As condições de contorno devem, quando possível, coincidir com os limites hidrogeológicos naturais (rios, lagos, divisor de águas, etc.). Em algumas situações não é possível utilizar os limites hidrogeológicos naturais no modelo matemático, principalmente quando os limites se encontram muito distantes da área de interesse. Entretanto, tais limites naturais tem que ser identificados quando da concepção do modelo conceitual.

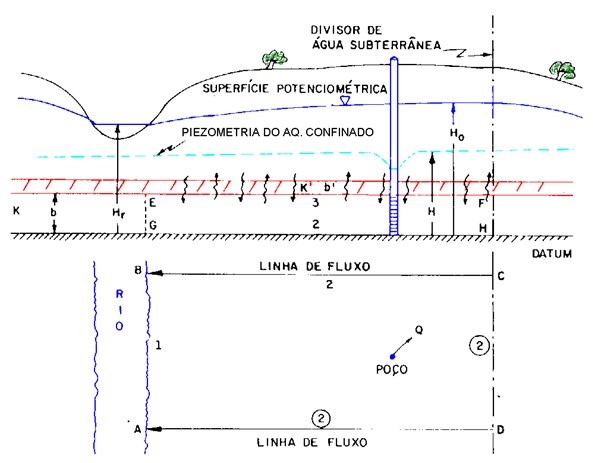
As condições de contorno podem ser classificadas em (CLEARY, 1989) de Carga ou de Direchlet, Fluxo ou de Neumann ou Misto, uma combinação das anteriores, conforme ilustra a Figura 2.

Figura 2 - Exemplos de condições de contorno. Exemplos de condições de contorno. 1 - Tipo: AB – carga constante para o aquífero freático; 2 - Tipo: BC, CD, AD – fluxo nulo para ambos os aquíferos; 2 - Tipo: GH – fluxo nulo para o aquífero confinado; 3 - Tipo: EF – drenança entre os aquíferos. (CLEARY, 1989)

No entanto, três passos são, necessariamente, seguidos na elaboração do modelo conceitual (ANDERSON & WOESSNER, 1994):

I. definição das unidade hidrogeológicas;

II. preparação do balanço hídrico;

III. definição do sistema de fluxo.

Existem vários modelos hidrogeológicos matemáticos disponíveis atualmente no mercado, podendo ser para estado estacionário ou transitório, aquífero confinado ou não confinado, em uma, duas ou três dimensões. Assim, para a escolha do modelo, deverão ser avaliadas as seguintes questões antes de sua adoção:

a) que atenda os objetivos pré-definidos;

b) que utilize os dados existentes ou possíveis de serem coletados;

c) que considere os dados existentes (anisotropias e/ou heterogeneidades);

d) se caso judicial, que o mesmo seja reconhecido pela justiça;

e) que possua histórico conhecido pela comunidade científica, para avaliação de suas limitações;

f) ser acessível, técnica e economicamente.

Uma vez escolhido o modelo, vamos ao trabalho!