Elaboração de modelo hidrogeológico numérico

Etapas para a Elaboração de um Modelo Hidrogeológico Matemático

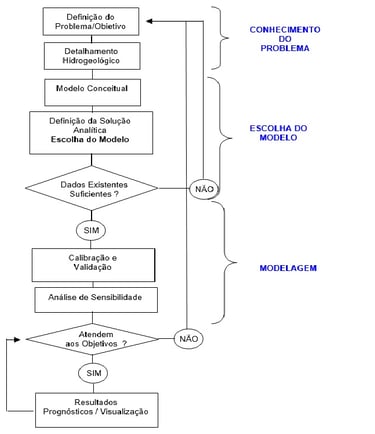
A elaboração de um modelo hidrogeológico matemático segue etapas sistemáticas que permitem representar de forma confiável o comportamento de aquíferos e sistemas de fluxo subterrâneo. Essas etapas estão resumidas no fluxograma da Figura 1 e descritas a seguir.

Figura 1 - Fluxograma de elaboração de modelo hidrogeologico numérico (MARCELINO 1998, modificado de CLEARY, 1991, ANDERSON & WOESSNER, 1994, WHB, 1998)

1. Conhecimento do Problema

1.1 Definição do Problema e Objetivo

Antes de aplicar qualquer metodologia científica, é fundamental compreender claramente o problema e os objetivos do estudo. Essa etapa permite identificar dificuldades, definir a metodologia adequada e organizar a coleta e análise de dados para fornecer soluções confiáveis.

1.2 Detalhamento Hidrogeológico

O modelo matemático reflete o conhecimento disponível sobre o sistema hidrogeológico, sendo confiável apenas na medida em que as informações inseridas forem precisas. Para isso, deve-se caracterizar o aquífero, suas camadas confinantes e parâmetros essenciais, como:

• Transmissividade (T): capacidade do aquífero de conduzir água.

• Coeficiente de armazenamento (S): capacidade de armazenar água.

• Velocidade e direção do fluxo: importantes em estudos de transporte de poluentes.

2. Escolha do Modelo Matemático

2.1 Modelo Conceitual

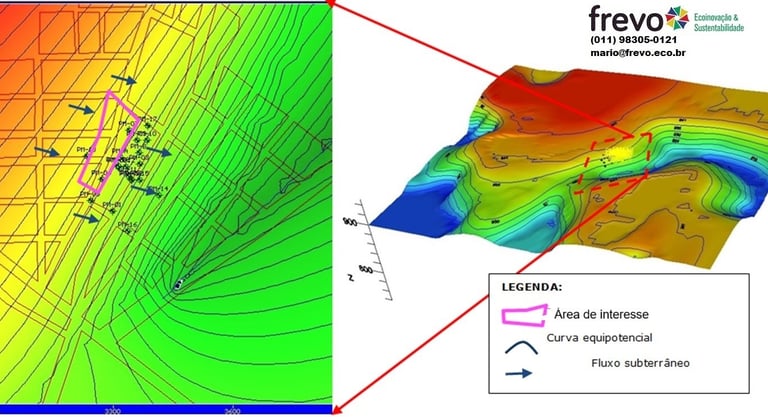
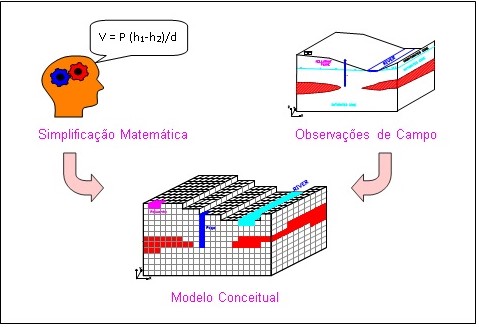
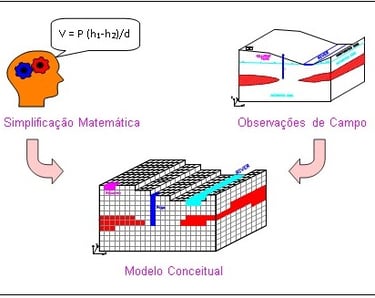
O modelo conceitual é uma representação simplificada do sistema hidrogeológico, geralmente em seção ou blocodiagrama. Ele organiza os dados de campo e permite analisar o sistema de forma realista (Figura 2).

Figura 2 - Processo de elaboração de modelo hidrogeológico numérico

Nos modelos numéricos, a variável dependente principal é a carga hidráulica, calculada em cada nó do modelo. A partir dela, é possível determinar velocidades de percolação usando a lei de Darcy e gerar mapas potenciais, delineando áreas de proteção de poços e trajetórias de contaminantes.

Basicamente os modelos numéricos irão calcular, de uma maneira geral, a carga hidráulica a cada intervalo de tempo em todos os nós, isto é, a variável dependente. A partir da carga hidráulica, são calculadas as velocidades de percolação, através da lei de Darcy. A apresentação normalmente é feita na forma gráfica de contorno, produzindo o mapa potenciométrico.

Diversos outros resultados podem ser conseguidos através do cruzamento dos dados, como por exemplo, na delineação de áreas de proteção de poços, onde o contorno é estabelecido em função do tempo de trânsito usando a distribuição de cargas, da condutividade hidráulica, porosidade efetiva e a lei de Darcy. No caso de estudos de transporte de partículas, as velocidades são calculadas em cada nó através da diferenciação numérica das cargas.

Assim, para a formulação do modelo conceitual deve-se definir a área de interesse e as condições iniciais e de contorno do modelo.

Condições iniciais e de contorno:

Para a resolução da equação numérica faz-se necessário a definição de uma condição inicial para o tempo igual a zero (h = hx,y,z,0). Segundo CLEARY (1989) esta informação normalmente é desconhecida, e muitos modeladores utilizam uma carga constante média. A fim de minimizar interferências de possíveis definições de carga constante errônea, é recomendável que a definição desta no modelo seja o mais distante possível da área de interesse (MARCELINO, 1997).

As condições de contorno devem, quando possível, coincidir com os limites hidrogeológicos naturais (rios, lagos, divisor de águas, etc.). Em algumas situações não é possível utilizar os limites hidrogeológicos naturais no modelo matemático, principalmente quando os limites se encontram muito distantes da área de interesse. Entretanto, tais limites naturais tem que ser identificados quando da concepção do modelo conceitual.

• Condição inicial: valor da carga hidráulica no tempo zero, geralmente estimado como média constante em regiões distantes da área de interesse.

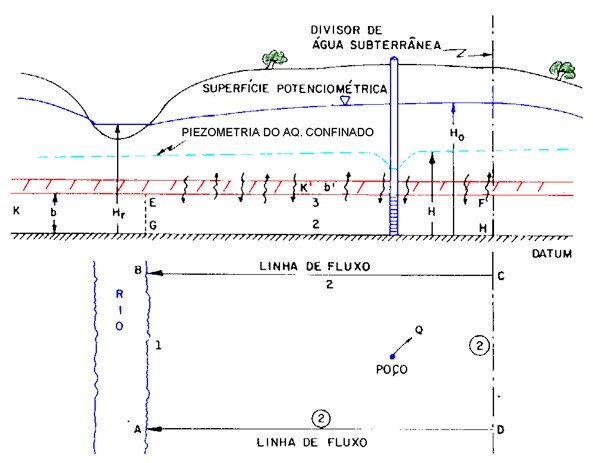
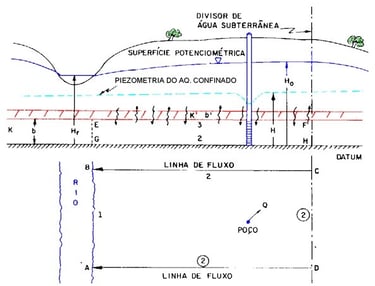
• Condições de contorno: devem coincidir, sempre que possível, com limites hidrogeológicos naturais (rios, lagos, divisores de água). Podem ser classificadas como (Figura 3):

  • Tipo Dirichlet (carga constante)

  • Tipo Neumann (fluxo constante)

  • Misto (combinação de carga e fluxo)

Figura 3 - Exemplos de condições de contorno. Tipo: AB – carga constante para o aqüífero freático; Tipo: BC, CD, AD – fluxo nulo para ambos os aqüíferos; Tipo: GH – fluxo nulo para o aqüífero confinado; Tipo: EF – drenança entre os aqüíferos. (CLEARY, 1989)

Passos do modelo conceitual (Anderson & Woessner, 1994):

1. Definir unidades hidrogeológicas;

2. Preparar balanço hídrico;

3. Definir sistema de fluxo.

2.2 Escolha do Modelo Numérico

Atualmente, existem diversos modelos numéricos, aplicáveis a estados estacionário ou transitório, aquíferos confinados ou não confinados, em uma, duas ou três dimensões. A escolha depende de:

• Adequação aos objetivos do estudo;

• Disponibilidade de dados;

• Consideração de anisotropias e heterogeneidades;

• Reconhecimento em casos judiciais;

• Histórico científico do modelo;

• Acessibilidade técnica e econômica.

Abordagem numérica:

• Diferenças finitas: fácil implementação, adequada a modelos bidimensionais, resultado pontual por nó, aceita heterogeneidades;

• Elementos finitos: mais detalhado, permite fluxos 3D totalmente anisotrópicos, usado em análises de transporte mais complexas.

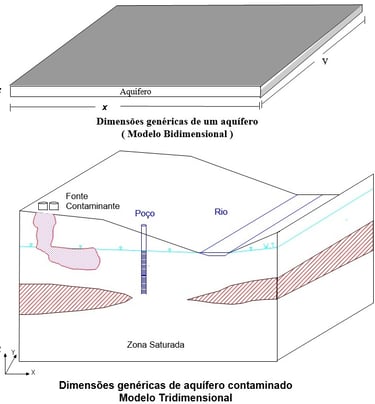
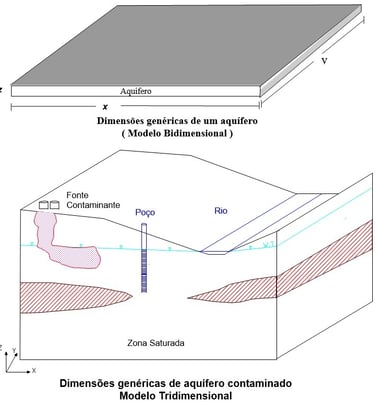
Para análises de fluxo geral, modelos bidimensionais são suficientes, já que os fluxos horizontais predominam. Em estudos de transporte de contaminantes, modelos tridimensionais são recomendados para capturar fluxos verticais importantes (Figura 4).

Figura 4 - Considerações das dimensões do aquífero a ser modelado na escolha do modelo matemático (MARCELINO, 1998)

3. Calibração e Validação

3.1 Calibração

A calibração ajusta o modelo para reproduzir as condições do campo, detectando e corrigindo erros. Dados de calibração devem ser representativos e de qualidade suficiente. Critérios de calibração podem ser:

Fluxo: forma da superfície potenciométrica, direções de fluxo, recarga, balanço hídrico.

Transporte: localização e histórico das fontes de contaminação, distribuição da pluma, coeficientes de dispersão e adsorção, taxa de degradação, concentrações.

Um modelo calibrado não garante representação única do sistema natural; a solução não é exclusiva e deve ser analisada com critérios qualitativos e quantitativos.

3.2 Validação

O modelo validado é aquele cujos prognósticos são confirmados em campo, comparando-se, por exemplo, a carga hidráulica prevista ou ensaios de vazão simulados com dados observados (Cleary, 1989).

4. Análise de Sensibilidade

A análise de sensibilidade avalia a influência de variações nos parâmetros do modelo, como condutividade hidráulica ou recarga. Ela ajuda a identificar incertezas e a priorizar parâmetros críticos para estudos futuros (Anderson & Woessner, 1994).

Referências Bibliográficas

• ANDERSON, M. P.; WOESSNER, W. W. Applied Groundwater Modeling: Simulation of Flow and Advective Transport. San Diego: Academic Press, 1994.

• CLEARY, R. W. Groundwater Modeling Guidelines for Site Investigation and Remedial Action. New York: Van Nostrand Reinhold, 1989.

• MARCELINO, M. Modelagem Matemática de Aquíferos: Conceitos e Aplicações. São Paulo: Universidade de São Paulo, 1998.

• WHB (Water Hydrogeological Bureau). Manual of Groundwater Modeling Techniques. Washington, D.C.: WHB Publications, 1998.